Girolamo Cardano discovered the formula needed to solve cubic equations and published it in his algebra book, Ars Magna. The formula is long and takes time to complete, but it works well sometiems. However, there is a problem that is interesting. Below is my work for part of it.
As you can see, it results with an imaginary number due to the square root of the negative number. When you perform the second portion of the equation it results in the cube root of 2-11i. Therefore, there is no real solutions to the equation. The interesting aspect of this problem is that it in fact does have three real solutions. I was intrigued by this and decided to investigate it more because Cardano's formula has worked for all other problems. I came across the work of Rafael Bombelli. He played around with the equation in order to find real solutions. Bombelli noticed that if you simply break apart the square root of -121 you can change it to the square root of 121*-1, which is the same as the square root of 121 multiplied by the square root of -1. We can now see that the reduced result of the cubic formula is now x= cube root of 2+11*sqrt(-1)+cube root of 2-11*sqrt(-1). Reducing this results in the (2+sqrt(-1))+(2-sqrt(-1)). The square roots will cancel each other out allowing us to find that one solution to this equation is 2+2=4. Once one solution has been found the others can be found using it to factor, so we would factor out x-4 from the original equation. Using algebra, we can find that the other two solutions is -2 + sqrt(3) and p-2 - sqrt(3).
Bombelli failed to find a formula that better fit solving cubic equations. Because of his failure he referred to his idea and approach as "a wild thought." He was unaware that it would take two more centuries to find out the actual answer to why Cardano's formula did now always work. It was the work of Euler and the discovery of calculus to find a solution. The found interest of this equation allowed mathematicians to see that there was more to learn about cubic equations and how to solve them. Over the centuries, the different mathematicians each used their knowledge to build on the already known information about solving cubic equations.
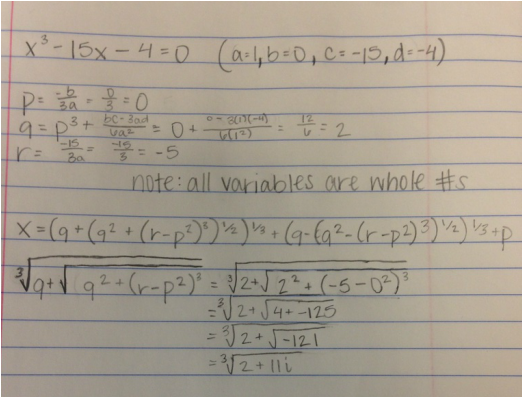
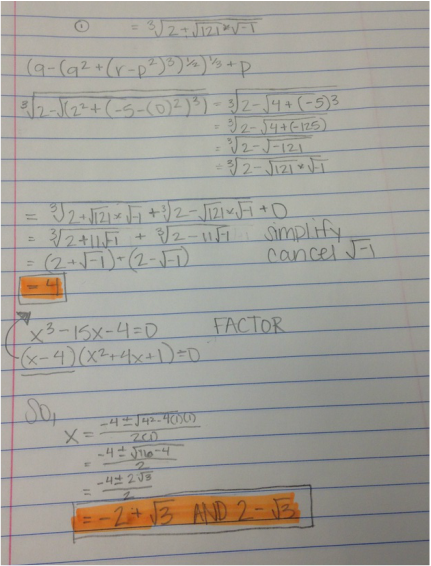
 RSS Feed
RSS Feed